ミニマックス法とは、今後現れうる局面をすべて得点化して、自分と相手が常に最善手を打った場合に、より自分の得点が高くなる選択をするアルゴリズムです。詳しくはミニマックス法 – Wikipediaで。

class TicTacToe():
    empty = ' '
    x = 'X'
    o = 'O'

    board = [[empty, empty, empty],
             [empty, empty, empty],
             [empty, empty, empty]]
    b = board

    def minimax(self, board, turn, depth):
        if depth == 0:
            score = self.eval(board)[0] - self.eval(board)[1]
            return (score)
        nextBoardsList = []
        for y in range(len(self.b)):
            for x in range(len(self.b[0])):
                if board[y][x] == self.empty:
                    tempBoard = deepcopy(board)
                    tempBoard[y][x] = turn
                    nextBoardsList.append( (tempBoard,(x, y)) )

        if not nextBoardsList:
            score = self.eval(board)[0] - self.eval(board)[1]
            return (score)

        best = False
        if turn == self.o:
            nextTurn = self.x
        else:
            nextTurn = self.o
        for i in nextBoardsList:
            result = self.minimax(i[0], nextTurn, depth-1)[0]
            if best:
                if turn == self.o and best[0] < result:
                    best = (result, i[1])
                elif turn == self.x and best[0] > result:
                    best = (result, i[1])
            else:
                best = (result, i[1])

        return best

minimax()は(得点, 最善手)のタプルを返す関数です。引数のboardは読みの対象となる現在の盤面、turnはマル・バツどちらのターンか、depthは何手先まで読むかの指定です。また、eval()は(先手（マル）の得点, 後手（バツ）の得点)を返す関数です。

        nextBoardsList = []
        for y in range(len(self.b)):
            for x in range(len(self.b[0])):
                if board[y][x] == self.empty:
                    tempBoard = deepcopy(board)
                    tempBoard[y][x] = turn
                    nextBoardsList.append( (tempBoard,(x, y)) ) 

まず、一手先の盤面をすべてリストにします。（そのまま書き換えるといろいろ面倒なことになるので、コピー（deepcopy()）してから書き換えたものをリストに追加し、またそのときの置いた場所も記録しておきます。）

        for i in nextBoardsList:
            result = self.minimax(i[0], nextTurn, depth-1)[0]
            if best:
                if turn == self.o and best[0] < result:
                    best = (result, i[1])
                elif turn == self.x and best[0] > result:
                    best = (result, i[1])
            else:
                best = (result, i[1])  

さっき作ったリストを対象に、もっとも得点の高い手を探すためにforループを回します。

で、ここがポイントなのですが、さらに次の手を局面を求めるために自分自身（minimax()）を呼び出します。ただ、最初に受け取った引数を同じように渡すと無限ループになってしまうので、読みの深さを指定するdepth変数を1減らし、読みの対象（board）に先ほど取得した「一手先の盤面」を指定します。

そうして求めた「一手先」をまたminimax()の引数として呼び出し……の繰りかえしが盤面のすべてが埋まるかdepthが0になるまで続きます。

        if depth == 0:
            score = self.eval(board)[0] - self.eval(board)[1]
            return (score)  

        if not nextBoardsList:
            score = self.eval(board)[0] - self.eval(board)[1]
            return (score)  

そのどちらかの条件を満たしたとき、初めて値が返されます。ここで返されている値は、先読みを最初に指定したdepthの数だけ繰り返して到達した盤面（またはすべてが埋まったときの盤面）を得点化したものです。

        return best  

最下層から値を返すと、一つ上の層のresultが確定できます。ループを完遂しもっともよい手bestが確定させ、return bestと返します。その値を元に再び一つ上の層でresultが確定し……と繰り返していきます。

僕はこのロジックを理解するのにかなり時間がかかったので、ちょっと図にしてみます。（セールで買ったOmniGraffleを使いたかったというのも）

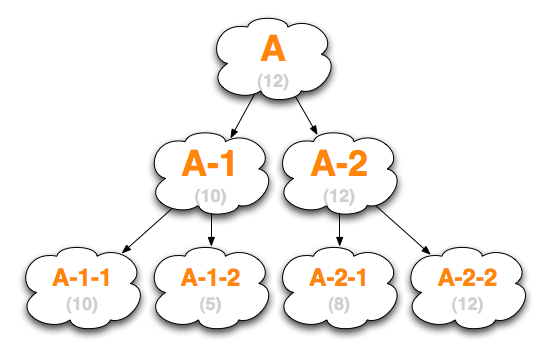
Aは現在の盤面です。A-1,A-2は現在の盤面から一手先を読んだときの盤面（二通りしかありませんが、実際はもっとたくさんあるはずです）、そのしたにあるのがさらに一手先を読んだときの盤面。この階層で読みを打ち切り、return (score)されたとします。

仮にA-1-1から返ってくる値を(10)、A-1-2が(5)とすると、A-1でのfor i in nextBoardsListループで導き出されるbestの値はA-1-1のものになります。これが確定すると、Aでのfor i in nextBoardsListも進み、今度はA-2のほうを計算することになります。A-2-1を(8)、A-2-2を(12)としましょう。A-2で確定されるbestの値はA-2-2になり、それをふまえた上で決定されるAでのbestの値もA-2-2になります。これが最初に呼び出されたminimax()としての結果になるわけです。

上手く説明できましたかね……？

ところで、僕が最初に書いたPythonスクリプトはCUIで遊ぶオセロでした。そのときのCPUはとにかくたくさんの石をとるだけの単純なものでしたが、今回のでこういうアルゴリズムを実装する楽しさがわかったので、また今度書き直してみようかと思います。

ちなみに、3×3のマルバツは現実的な時間ですべての局面を読み切ることができて、双方が最善を尽くすと必ず引き分けになることがわかっています。一方8×8のオセロはまだそこまで研究が進んでいないので、プログラムの強さを高めるという楽しみ方もできそうです。競うレベルまで到達するのはなかなか大変そうですが……。